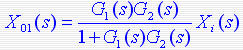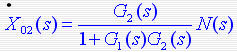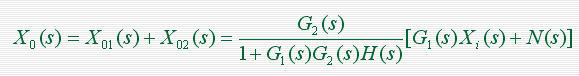|
一、系统方框图 自动控制网www.eadianqi.com版权所有
系统方框图是系统中各个环节的功能和信号流向的图形表示方法。 自动控制网www.eadianqi.com版权所有
方框图是控制系统的又一种数学模型。
特点:具有图示模型的直观,具有数学模型的精确性。方框图具有数学性质,可以进行代数运算和等效变换,是计算系统传递函数的有力工具,应用非常普遍。
说明
1)一个方框代表系统的一个组成环节;
2)方框图中的环节是以无负载效应为前提的(即前一个环节的输出不受后一个环节的影响);
3)表示系统结构情况的物理框图与系统方框图是有区别的。
结构要素
1)信号线:带有箭头的直线,箭头表示信号的传递方向,直线旁标记信号的时间函数或象函数。

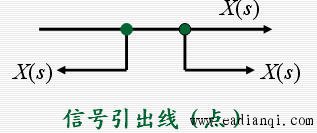
2)信号引出线(点):表示信号引出或测量的位置(该位置称为引出点),同一信号线上引出的信号,其性质、大小完全相同。
3)函数框图(环节):传递函数的图解表示(方框中表示的输入与输出之间环节的传递函数)。
 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
4)求和点(比较点):信号之前代数加减运算的图解。
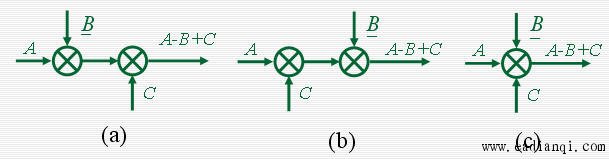
求和点(比较点)
任何系统都可以由信号线、函数框图、信号引出线和求和点组成的方框图来表示。
方框图的建立步骤
1)建立系统各个部件的微分方程,明确信号的因果关系(输入/输出);
2)对上述微分方程进行拉氏变换,绘制各部件的方框图;
3)按照信号在系统中的传递、变换过程,依次将各部件的方框图连接起来,得到系统的方框图。
系统方框图的简化
1)方框图的运算法则
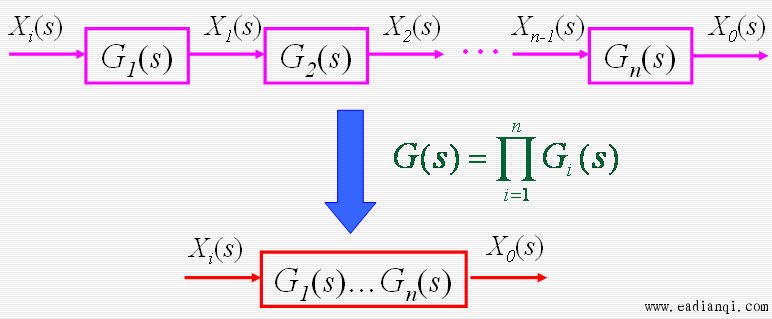
a. 串联连接
c. 反馈连接
下图是一个具有反馈联接的最基本的闭环系统
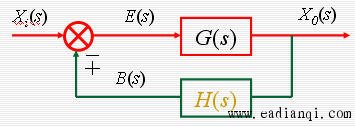
G(s) - 前向通道传递函数 H(s) - 反馈回路传递函数
E(s) - 偏差信号 B(s) - 反馈信号
E(s)= Xi(s)- B(s) 自动控制网www.eadianqi.com版权所有
显然: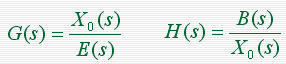
前向通道的传递函数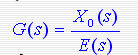
反馈通道的传递函数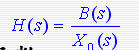
开环系统的传递函数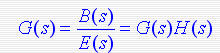
闭环系统的传递函数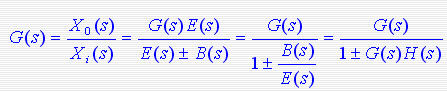
若H(s)=1,则此闭环系统为单位反馈系统,其闭环传递函数为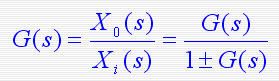
注意:
这里的开环传递函数、反馈通道传递函数和前向通道传递函数都是一个闭环系统中的一部分元件或环节的传递函数,二闭环传递函数才是这个闭环系统的传递函数。表示闭环系统内各种传递函数的符号只是一个符号而已。
干扰作用下的闭环系统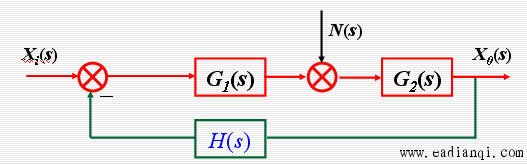 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
在输入Xi(s)的作用下: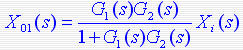
在输入N(s)的作用下: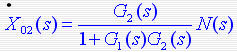
则整个闭环系统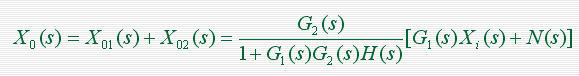
结论
1)在上式中,若取|G1(s)H(s)|>>1,且|G1(s) G2(s) H(s)|>>1,则干扰所引起的输出趋于0。尽管系统在运行过程中,干扰是不可避免的,但对于反馈控制系统,只要系统参数选择适当,就可以使系统具有很强的抗干扰能力。
2)对于同一个闭环系统,当输入的取法不同时,其前向通道和反馈回路的传递函数的不同的,系统的传递函数也是不同的,但传递函数的分母不变。这说明了系统传递函数的分母确实反映了系统本身的固有特性,这个特性与外界无关。而这以结论对开环系统并不适用。
传递函数方框图等效的基本规则
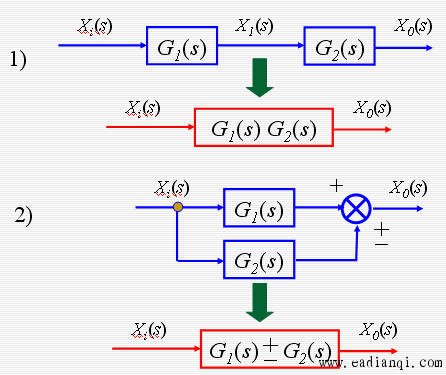
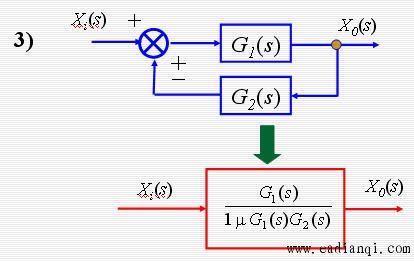 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
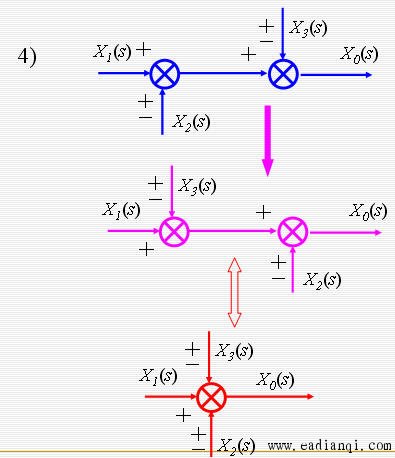
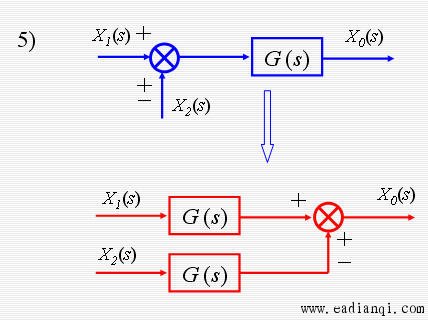
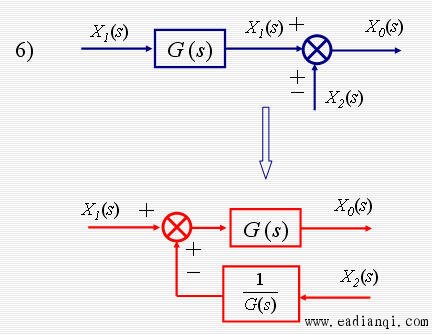
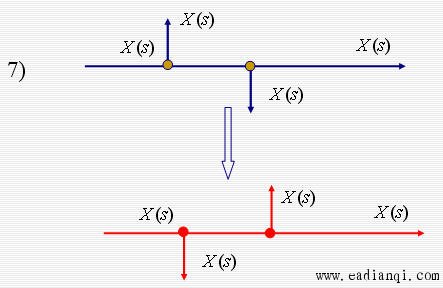
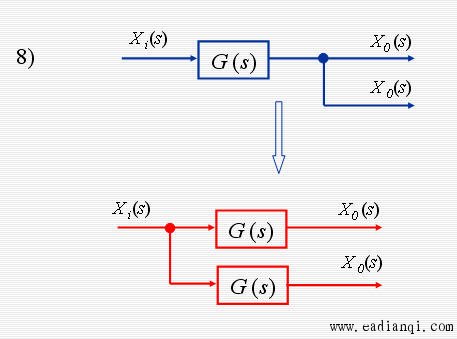
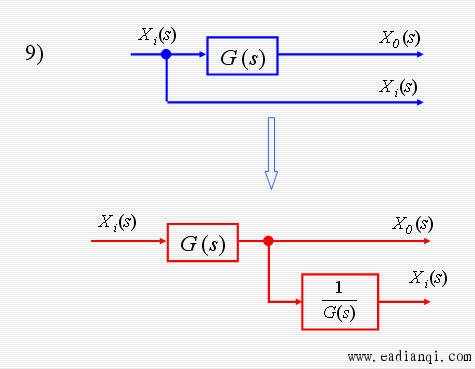
系统方框图简化实例
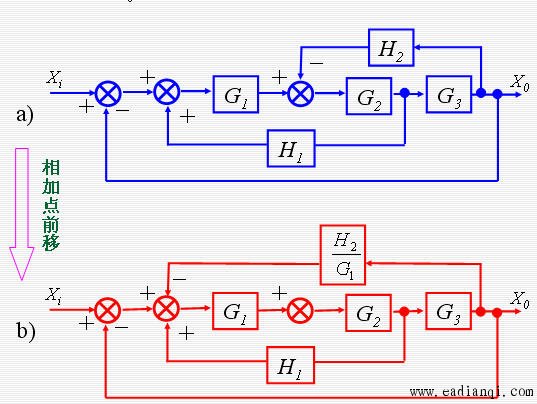
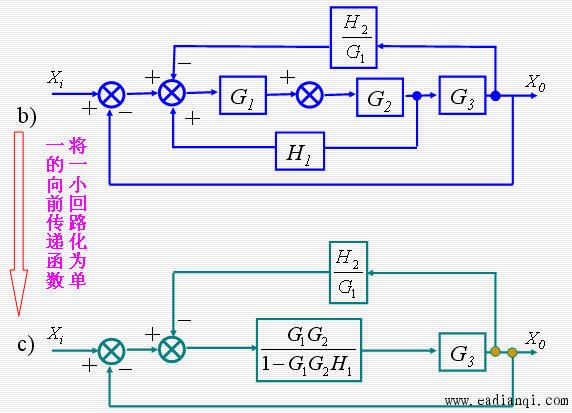
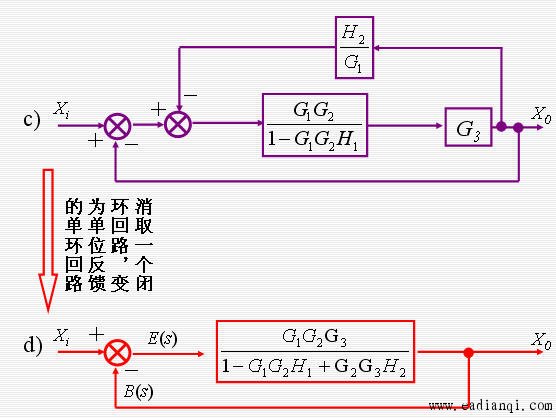
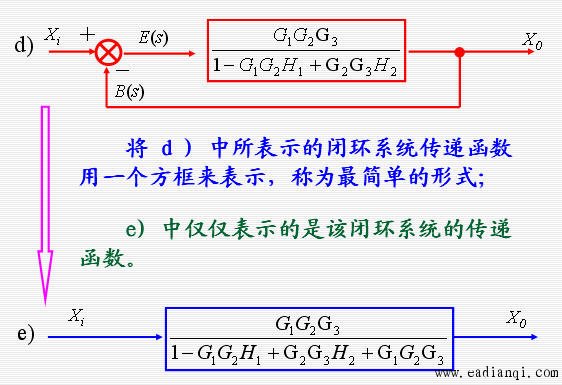 本文来自www.eadianqi.com
传递函数方框图简化的一般步骤
1)确定系统的输入量和输出量。
如果作用在系统的输入量有多个,则必须分别对每一个输入量(此时,假设其他输入均为零),逐个进行简化,求得各自的传递函数。对于具有多个输出量的情况,也要分别进行变换,求取各自的传递函数。
2)若方框图中有无交叉的多个回路,则按照先里后外的原则,逐个简化,直到简化成一个方框的形式。若方框图中有交叉的连接,用如下的方法:
方法一:若系统的传递函数方框图同时满足以下两个条件:
条件1,整个系统方框图中只有一条前向通道;
条件2,各局部反馈回路间存在公共的传递函数方框,
则可以直接用下列公式求解:
括号内每一项的符号是这样决定的:在相加点处,对反馈信号为相加时取负号,对反馈信号为相减时取正号。
方法二:若系统的传递函数方框图不同时满足以上两个条件,则可通过相加点、分支点的前后移动等法则,将系统传递函数方框图化为同时满足以上两个条件的形式,然后应用上式即可。
方法三:若系统的传递函数方框图不同时满足以上两个条件,可通过相加点、分支点的前后移动等法则,将交叉消除,简化成无交叉的多回路形式。然后由里到外进行变换直到变换成一个单一回路或一个方框的形式,最后写出系统的传递函数。 自动控制网www.eadianqi.com版权所有
系统方框图简化实例
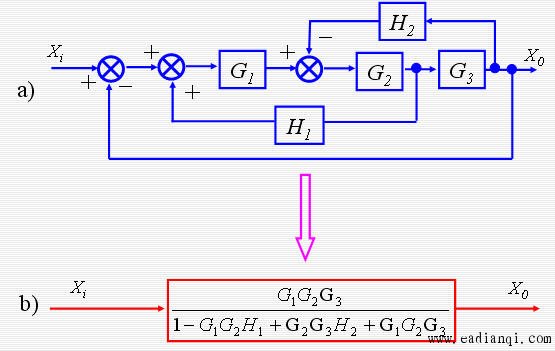 自动控制网www.eadianqi.com版权所有
|




 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 


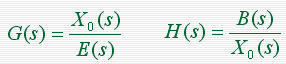
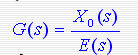
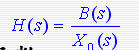
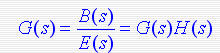
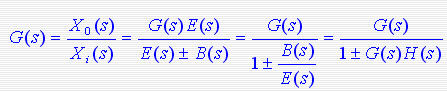
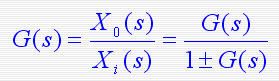
 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有