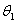 、 、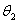 、 、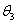 分别为轴I、Ⅱ、Ⅲ在输入转矩 分别为轴I、Ⅱ、Ⅲ在输入转矩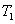 、 、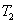 、 、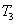 的作用下产生的扭转角。根据动力平衡原理和传动关系有 自动控制网www.eadianqi.com版权所有 的作用下产生的扭转角。根据动力平衡原理和传动关系有 自动控制网www.eadianqi.com版权所有
由于丝杠和工作台之间轴向弹性变形使轴Ⅲ附加了一个扭转角
将 本文来自www.eadianqi.com
将各轴的扭转角折算到轴I上得轴I的总扭转角 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
将 本文来自www.eadianqi.com
式中 本文来自www.eadianqi.com
4、建立系统的数学模型 本文来自www.eadianqi.com 根据以上的参数折算,建立系统动力平衡方程和推导数学模型。 本文来自www.eadianqi.com
设输入量为轴I的输入转角Xi;输出量为工作台的线位移Xo。根据传动原理,把Xo折算成轴I的输出角位移
本文来自www.eadianqi.com
又因为 因此,动力平衡关系可以写成下式 本文来自www.eadianqi.com
这就是机床进给系统的数学模型,它是一个二阶线性微分方程。其中
式中
将S=j 自动控制网www.eadianqi.com版权所有
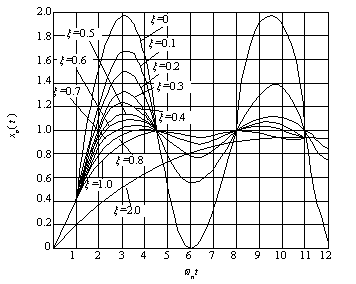
自动控制网www.eadianqi.com版权所有 图2-13 二阶系统单位阶跃响应曲线 自动控制网www.eadianqi.com版权所有
|
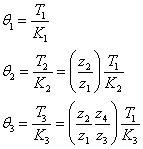 本文来自www.eadianqi.com
本文来自www.eadianqi.com 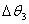 ,因此轴Ⅲ上的实际扭转角
,因此轴Ⅲ上的实际扭转角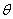 Ⅲ为:
Ⅲ为: 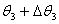 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 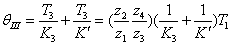 本文来自www.eadianqi.com
本文来自www.eadianqi.com 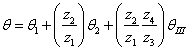
 值代入上式有:
值代入上式有: 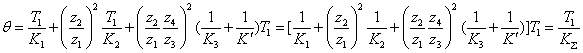 (2-19)
(2-19) 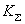 ——折算到轴I上的总扭转刚度系数
——折算到轴I上的总扭转刚度系数 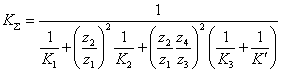 (2-20)
(2-20)  。在轴I上根据动力平衡原理有 本文来自www.eadianqi.com
。在轴I上根据动力平衡原理有 本文来自www.eadianqi.com 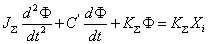 (2-21)
(2-21)  (2-22)
(2-22) 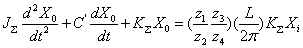 (2-23) 本文来自www.eadianqi.com
(2-23) 本文来自www.eadianqi.com 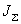 、
、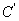 、
、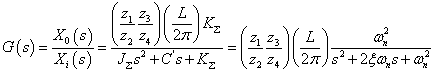 (2-24) 本文来自www.eadianqi.com
(2-24) 本文来自www.eadianqi.com 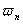 ——系统的固有频率,
——系统的固有频率,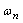 =
=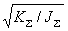 (2-25) 本文来自www.eadianqi.com
(2-25) 本文来自www.eadianqi.com 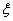 ——系统的阻尼比,
——系统的阻尼比,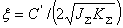 (2-26) 本文来自www.eadianqi.com
(2-26) 本文来自www.eadianqi.com 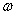 代入(2-24)可求出A(
代入(2-24)可求出A(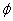 (
(