测试模态下，系统的等效框图如图所示。确定系统的振荡频率ωc与增益Kc有多种方法，比较常用的是描述函数法，此方法实际上是根据非线性环节输入信号与输出信号之间基波分量关系来进行近似的一种有效方法。 图 继电反馈系统结构图 ①非线性特征的描述函数N(A)是指：当输入时正弦信号Asin(ωt)时，输出的基波分量Ysin(ωt+φ)对输入正弦量的复数比，即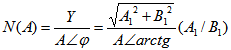：  其中A1、B1是输出Y(t)的傅立叶级数的一次项系数。实际的带有回环的节点非线性环节特性的描述函数可以表示为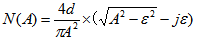：  公式中A为正弦波幅值，d为回环幅值，ε为回环宽度的一半。②由极限环振荡确定被控对象特征参数 设被控对象的传递函数为如下形式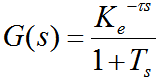：  本文来自www.eadianqi.com 其中K为对象的增益，T为对象的时间常数，τ为对象的滞后时间。 考虑由具有传递函数G(s)的对象和具有继电特性的反馈部分组成的简单反馈系统如图2所示。这时系统的闭环特征方程发生振荡的条件可以写成：1+N(A)G(s)=0 (s=jωc)，即G(jωc)=-1/N(A)。 设该等式的实部和虚部均为零，则可得出振荡频率Wc的增益Kc，在这里只考虑一种简单的情况，假设继电特征非线性环节不带有回环，即若设ε=0，则描述函数可以化简成N(A)=4d/πAc，临界振荡周期Tc=2π/ωc可通过直接测量输出相邻峰值的时间确定。 |