|
一、拉普拉斯变换 把一个时间函数f(t)变换为另一个变量S的函数F(S),变换如下进行: 用下列符号表示它们之间的关系: 二、传递函数 利用微分方程分析自动控制系统的方法称为时域分析; 利用传递函数分析自动控制系统的方法称为频域分析。 传递函数定义: 在零初始条件下,线性常系数系统的输出量的拉普拉斯变换式与输入量的 拉普拉斯变换式之比。 用公式表达传递函数: 其中:W(S)为传递函数, X0(S)为输出量的拉普拉斯变换式, Xi(S)为输入量的拉普拉斯变换式 三、几个典型环节的传递函数 自动控制网www.eadianqi.com版权所有 1.比例环节 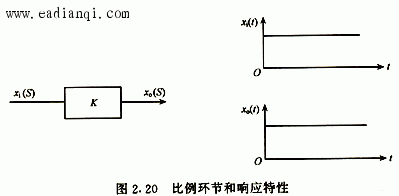 2.惯性环节 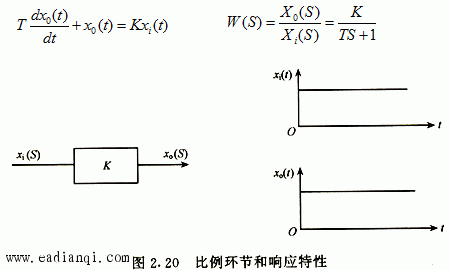 3.积分环节 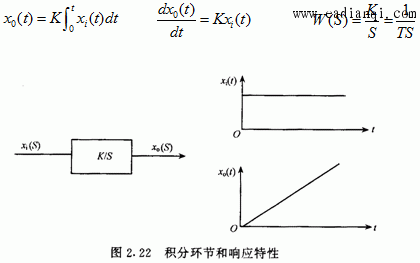 4.震荡环节 微分方程 传递函数 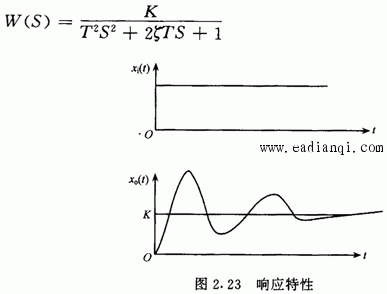 5.实际微分环节 微分方程 传递函数 本文来自www.eadianqi.com 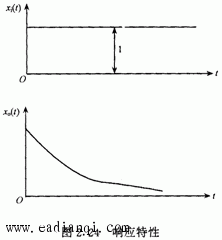 6.延迟环节 微分方程 传递函数 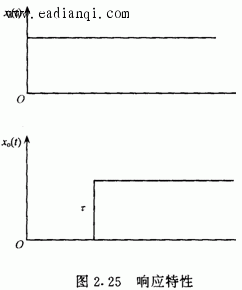 四、环节的连接和方块图变的换 由于系统由多重环节的不同连接组合起来,因此为了求系统的传递函数,必须要清楚环节的连接形式和它们的关系。实际上,不管系统中各环节之间的连接有多复杂,但从分析上看,环节之间有三种基本连接方式,即串联、并联和反馈,而方块图就是用来表示这些环节是怎样连接起来的。 1.串联 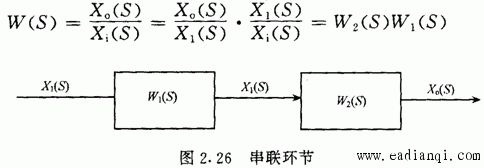 2.并联 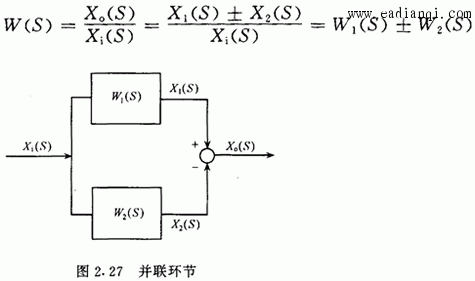 自动控制网www.eadianqi.com版权所有 3. 反馈连接 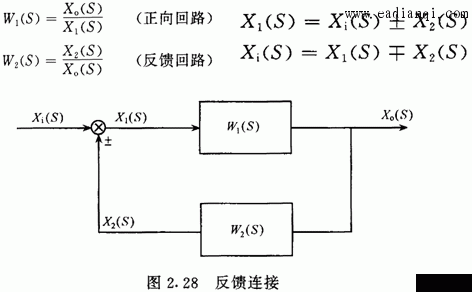 五、控制器的控制规律及响应特性 1. 比例控制规律(P) 2.比例积分控制规律(PI) 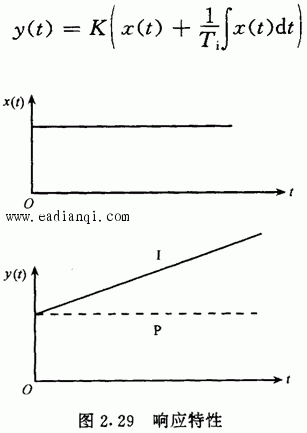 3.比例微分控制规律(PD) 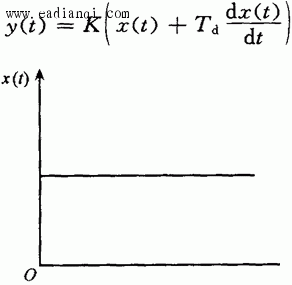 4.比例积分微分控制规律(PID) 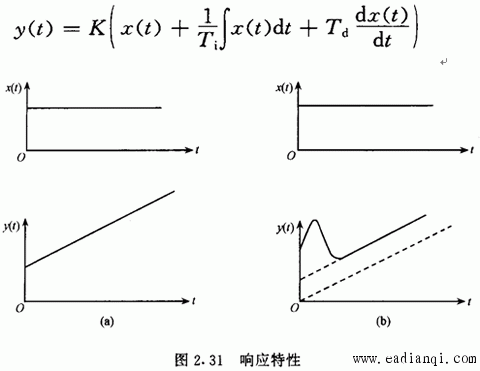 |