在零初始条件下，线性定常系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比，定义为线性定常系统的传递函数。 即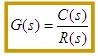， 若已知线性定常系统的微分方程为 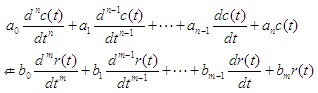 式中 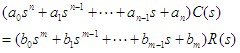 为输出量， 为输入量 。设 和及其各阶导数初始值均为零，对上式取拉氏变换，得 则系统的传递函数为 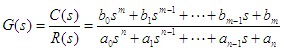 自动控制网www.eadianqi.com版权所有 或写为  传递函数与输入、输出之间的关系，可用图表示。 传递函数的特点 1.作为一种数学模型，传递函数只适用于线性定常系统，这是由于传递函数是经拉普拉斯变换导出的，而拉氏变换是一种线性积分运算。 2.传递函数是以系统本身的参数描述的线性定常系统输入量与输出量的关系式，它表达了系统内在的固有特性，只与系统的结构、参数有关，而与输入量或输入函数的形式无关。 3.传递函数可以是无量纲的，也可以是有量纲的，视系统的输入、输出量而定，它包含着联系输入量与输出量所必须的单位，它不能表明系统的物理特性和物理结构。许多物理性质不同的系统，有着相同的传递函数，正如一些不同的物理现象可以用相同的微分方程描述一样。 4.传递函数只表示单输入和单输出(SISO)之间的关系，对多输入多输出(MIMO)系统，可用传递函数阵表示。 5.传递函数可表示成  式中  为分母多项式的根，称为传递函数的极点； 为分子多项式的根，称为传递函数的零点； 自动控制网www.eadianqi.com版权所有 6.传递函数分母多项式称为特征多项式，记为  而D(s)=0称为特征方程。传递函数分母多项式的阶次总是大于或等于分子多项式的阶次，即n≥m。 典型环节的传递函数 控制系统由许多元件组合而成，这些元件的物理结构和作用原理是多种多样的，但抛开具体结构和物理特点，从传递函数的数学模型来看，可以划分成几种典型环节，常用的典型环节有： 比例环节 惯性环节 积分环节 微分环节 振荡环节 延迟环节 1.比例环节 环节输出量与输入量成正比，不失真也无时间滞后的环节称为比例环节。输入量与输出量之间的表达式为  比例环节的传递函数为  式中K为常数，称为比例环节的放大系数或增益。 2.惯性环节(非周期环节) 自动控制网www.eadianqi.com版权所有 惯性环节的动态方程是一个一阶微分方程  其传递函数为  式中T —— 惯性环节的时间常数 K —— 惯性环节的增益或放大系数 当输入为单位阶跃函数时，其单位阶跃响应为 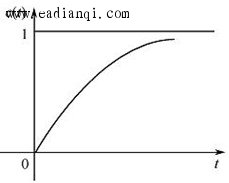 单位阶跃响应曲线 当输入为单位阶跃函数时，其单位阶跃响应为  3.积分环节 输出量正比于输入量的积分的环节称为积分环节，其动态特性方程  其传递函数  本文来自www.eadianqi.com 式中  为积分时间常数。积分环节的单位阶跃响应为  它随时间直线增长，当输入突然消失，积分停止，输出维持不变，故积分环节具有记忆功能，如图所示。 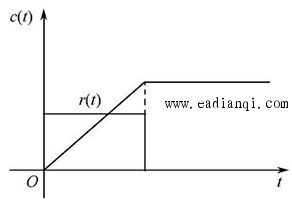 4.微分环节 理想微分环节的特征输出量正比于输入量的微分，其动态方程  其传递函数  式中  称微分时间常数它的单位阶跃响应曲线  自动控制网www.eadianqi.com版权所有 如图所示，理想微分环节实际上难以实现，因此我们常采用带有惯性的微分环节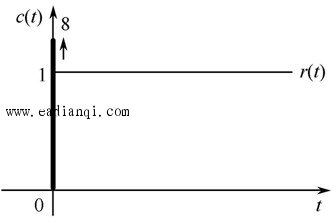，  其传递函数  其单位阶跃响应为  曲线如下图所示，实际微分环节的阶跃响应是按指数规律下降，若K值很大而 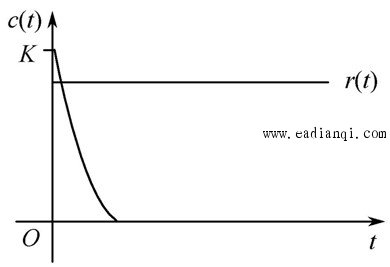值很小时，实际微分环节就愈接近于理想微分环节。 5.二阶振荡环节 二阶振荡环节的动态方程为  其传递函数 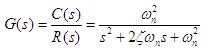 本文来自www.eadianqi.com 式中  为无阻尼自然振荡频率，ξ为阻尼比，在后面时域分析中将详细讨论。6. 延迟环节(时滞环节) 延迟环节是输入信号加入后，输出信号要延迟一段时间τ后才重现输入信号，其动态方程为  其传递函数是  式中τ称延迟时间 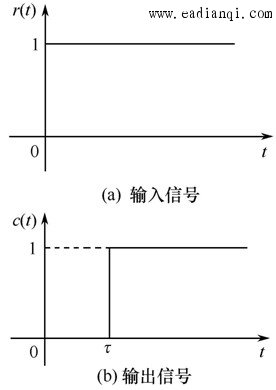 需要指出，在实际生产中，有很多场合是存在迟延的，比如皮带或管道输送过程、管道反应和管道混合过程，多个设备串联以及测量装置系统等。迟延过大往往会使控制效果恶化，甚至使系统失去稳定。 |