|
线性化的基本方法是:将非线性函数在平衡状态或参考轨迹附近展开成泰勒级数,只保留线性项从而将非线性模型线性化;而被忽略的泰勒级数的高阶项必须足够小,因此这种方法又称为小信号分析 ( 或小扰动 ) 理论。
1. 非线性静态特性的线性化 本文来自www.eadianqi.com
本文来自www.eadianqi.com
本文来自www.eadianqi.com
忽略其高次幂项 本文来自www.eadianqi.com
写成线性模型的习惯表示形式: 自动控制网www.eadianqi.com版权所有
Y=Kx 本文来自www.eadianqi.com
2. 非线性微分方程的线性化 本文来自www.eadianqi.com
本文来自www.eadianqi.com
将非线性向量函数 f(x , u , t) 在参考状态轨迹附近展开成泰勒级数: 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 和 自动控制网www.eadianqi.com版权所有
为非线性状态方程在参考轨迹处的雅可比 (Jacobi) 矩阵, 从而导出非线性控制系统 在参考轨迹附近的线性化状态方程为 本文来自www.eadianqi.com
|
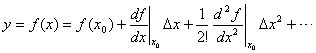
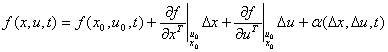

 本文来自www.eadianqi.com
本文来自www.eadianqi.com