|
1.稳定性定义: 若线性控制系统在初始扰动的影响下,其动态过程随时间的推移而逐渐衰减并趋于零(原平衡工作点),则称系统渐近稳定,简称稳定。反之,若在初始扰动影响下,系统的动态过程随时间的推移而发散,则称系统不稳定。 自动控制网www.eadianqi.com版权所有 2.线性系统稳定的充分必要条件 自动控制网www.eadianqi.com版权所有 [说明]:线性系统的稳定性仅取决于系统的自身的固有特性,而与外界条件无关。 本文来自www.eadianqi.com
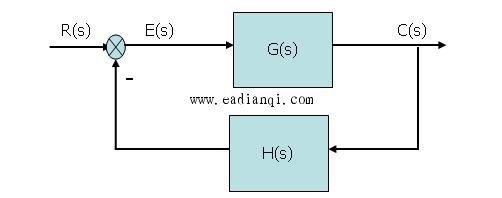
把δ(t)作为扰动信号,即:r(t)=δ(t)—Why? 自动控制网www.eadianqi.com版权所有 并假设系统为零初始状态。 本文来自www.eadianqi.com 闭环传递函数: 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 分析: 自动控制网www.eadianqi.com版权所有
(1)当且仅当系统的所有特征根都具有负实部时,才存在: 本文来自www.eadianqi.com
~系统收敛于原平衡工作点,即系统才稳定。 自动控制网www.eadianqi.com版权所有
(2)若特征根中有一个或一个以上的正实部根,则 (3)若特征根中有一个或一个以上的零实部根,而其余特征根均为负实部,则:脉冲响应c(t)→常数,或为等幅正弦振荡~临界稳定。 自动控制网www.eadianqi.com版权所有 |



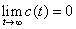
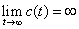 ,系统不稳定。
,系统不稳定。