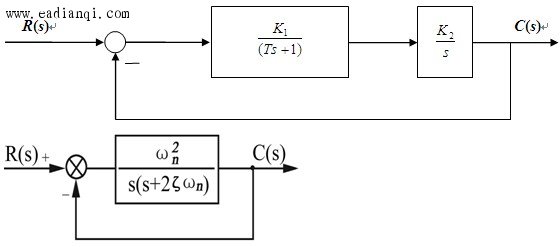
 开环传递函数  闭环传递函数 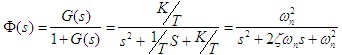 其中  ——系统的阻尼比 ——系统的无阻尼自然振荡角频率系统的闭环特征方程为  系统的两个闭环极点为  1 ζ>1 s1,2 是两个不相等的负实数极点 2 ζ=1 s1,2 是两个相等的负实数极点 3 0<ζ <1 s1,2 是一对具有负实部的共轭复数极点 自动控制网www.eadianqi.com版权所有 4 ζ=0 s1,2 是一对纯复数极点 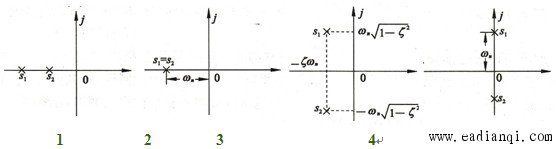 1. 当 ζ>1 时，系统有两个不相等的负实根，称为过阻尼状态。 两个不相等的负实根为  2. 当阻尼比ζ=1 时，系统的特征根为两相等的负实根，称为临界阻尼状态。 系统的超调量δ%=0。 3. 当 0<ζ<1 时，系统有一对实部为负的共轭复根，称为欠阻尼状态。 在欠阻尼状态下，系统的两个闭环极点为一对共轭复极点，即  其中，  称为阻尼振荡角频率。评价控制系统性能的从以下两个方面： 1 过渡过程的平稳性 2 过渡过程的快速性 典型二阶系统动态性能指标 本文来自www.eadianqi.com   0<ζ<1欠阻尼情况下 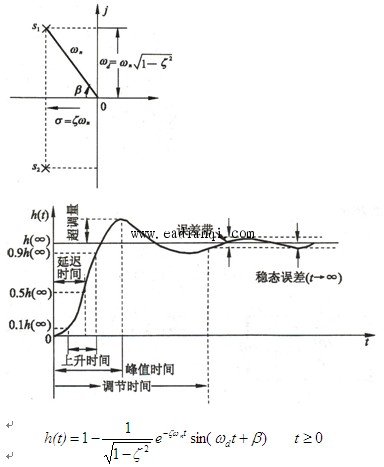 1．上升时间tr： 从零时刻首次到达稳态值的时间,即阶跃响应曲线从t=0开始第一次上升到稳态值所需要的时间。  2. 峰值时间tp ： 从零时刻到达峰值的时间，即 阶跃响应曲线从t=0开始上升到第一个峰值所需要的时间。  3. 超调量δ%： 阶跃响应曲线的最大峰值与稳态值的差与稳态值之比，即 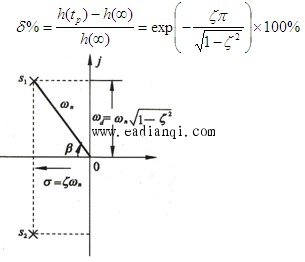 自动控制网www.eadianqi.com版权所有 β——阻尼角 OS1——等阻尼线  4. 调节时间ts：阶跃响应曲线进入允许的误差带(一般取稳态值附近±5%或±2%作为误差带)并不再超出该误差带的最小时间，称为调节时间(或过渡过程时间)。 误差带范围为 ±5%  误差带范围为± 2%  改善典型二阶系统动态性能的方法 1 加入开环零点 2 引入局部反馈 |