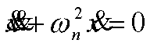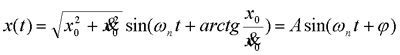|
线性系统与非线性系统的本质区别: 线性系统可以应用线性叠加原理;描述非线性系统运动的数学模型为非线性微分方程,故非线性系统不能应用叠加原理。 非线性系统的运动主要特点: (1)稳定性分析复杂 A 线性系统的稳定性 按照平衡状态的定义,对于线性系统,只有一个平衡状态y=0,线性系统的稳定性即为该平衡状态的稳定性,只取决于系统本身的结构和参数,与外作用和初始条件无关。
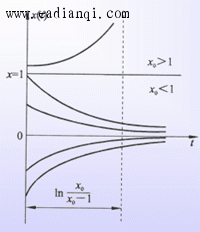
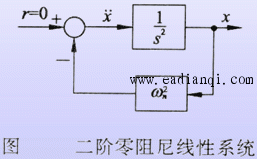
由此可见,非线性系统可能存在多个平衡状态,各平衡状态可能是稳定的也可能是不稳定的。初始条件不同,自由运动的稳定性亦不同。更重要的是,平衡状态的稳定性不仅与系统的结构和参数有关,而且与系统的初始条件有直接的关系。 (2)可能存在自激振荡现象 线性定常系统只有在临界稳定的情况下才能产生周期运动。考虑下图所示系统,设初始条件 x(0)=x0,x(0)=x0 系统自由运动方程为
自动控制网www.eadianqi.com版权所有 能维持。所以线性系统在无外界周期变化信号作用时所具有的周期运动不是自激振荡。
(3)频率响应发生畸变 非线性系统的频率响应除了含有与输入同频率的正弦信号分量(基频分量)外,还含有关于ω的高次谐波分量,使输出波形发生非线性畸变。若系统含有多值非线性环节,输出的各次谐波分量的幅值还可能发生跃变。 |