控制系统的频率响应常有三种表达形式,即
(1)将频率响应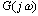 通过其幅频特性 通过其幅频特性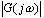 及相频特性 及相频特性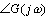 表示在极坐标中的图形,称为幅相图,或Nyquist图。本节将介绍各种典型环节的幅相图。 表示在极坐标中的图形,称为幅相图,或Nyquist图。本节将介绍各种典型环节的幅相图。
(2)在对数坐标中将频率响应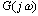 的幅频特性 的幅频特性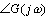 及相频特性 及相频特性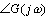 分开来表示的图形,称为对数频率特性,或Bode图。将在第三节中介绍。 分开来表示的图形,称为对数频率特性,或Bode图。将在第三节中介绍。
(3)将构成对数频率特性的幅频特性和相频特性集中绘制于一图,称为对数幅相图,或Nichols图。 自动控制网www.eadianqi.com版权所有

 Nyquist图 Nyquist图
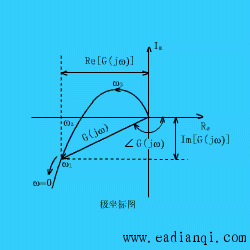
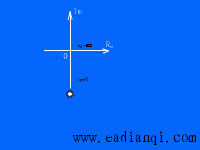
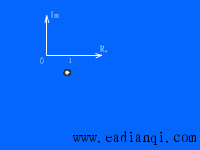
频率特性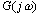 的极坐标图是当 的极坐标图是当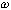 由零变化到无穷大时,表示在极坐标上的 由零变化到无穷大时,表示在极坐标上的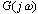 幅值与 幅值与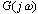 相角的关系图。因此,极坐标图是当 相角的关系图。因此,极坐标图是当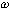 由零变化到无穷大时矢量 由零变化到无穷大时矢量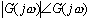 的轨迹。下图所示为极坐标图的例子。在极坐标图上, 的轨迹。下图所示为极坐标图的例子。在极坐标图上,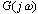 的每一点都表示一特定 的每一点都表示一特定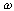 值的向量端点。 值的向量端点。 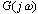 在实轴上的投影是 在实轴上的投影是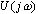 ,在虚轴上的投影是 ,在虚轴上的投影是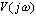 。注意,在极坐标图上,正(或负)相角是从正实轴开始以反时针旋转(或正时针旋转)来定义的。极坐标图通常称为Nyquist图。在极坐标图上,能显示出轨迹上的频率分布。采用极坐标图,可以在一张图上描绘出整个频率域的频率响应特性。 。注意,在极坐标图上,正(或负)相角是从正实轴开始以反时针旋转(或正时针旋转)来定义的。极坐标图通常称为Nyquist图。在极坐标图上,能显示出轨迹上的频率分布。采用极坐标图,可以在一张图上描绘出整个频率域的频率响应特性。 自动控制网www.eadianqi.com版权所有

 放大环节的频率响应 放大环节的频率响应
放大环节也称比例环节,其传递函数为
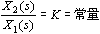
由传递函数求得放大环节的幅频特性及相频特性为
 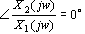
可见,放大环节的幅频特性与相频特性都是与角频率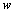 无关的常量。(点击图片) 无关的常量。(点击图片) 自动控制网www.eadianqi.com版权所有


 积分环节的频率响应 积分环节的频率响应
积分环节的传递函数为
 
其频率响应为
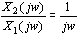 
由频率响应求得其幅频特性及相频特性分别为
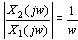  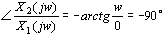 本文来自www.eadianqi.com
当角频率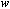 由0变到 由0变到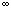 时,积分环节的幅频特性由无穷大衰减到零,其相频特性为与 时,积分环节的幅频特性由无穷大衰减到零,其相频特性为与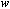 无关的常量 无关的常量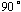 。 。

 惯性环节的频率响应 惯性环节的频率响应
惯性环节的传递函数为
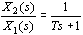 自动控制网www.eadianqi.com版权所有
式中T——惯性环节的时间常数,量纲为s。
由传递函数求的惯性环节的幅频特性及相频特性为
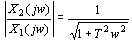 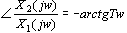
当 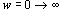 时,惯性环节的幅频特性由1衰减到0,在 时,惯性环节的幅频特性由1衰减到0,在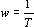 处,其值为 处,其值为 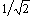 ;相频特性由 ;相频特性由 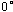 变到 变到 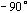 ,在 ,在 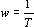 处,其值为 处,其值为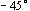 。 本文来自www.eadianqi.com 。 本文来自www.eadianqi.com


 振荡环节的频率响应 振荡环节的频率响应
振荡环节的传递函数为
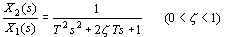
式中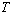 ——振荡环节的时间常数; ——振荡环节的时间常数;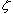 ——振荡环节的阻尼比。 ——振荡环节的阻尼比。
由传递函数求的振荡环节的幅频特性及相频特性为
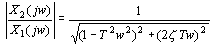 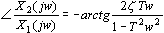 本文来自www.eadianqi.com 本文来自www.eadianqi.com
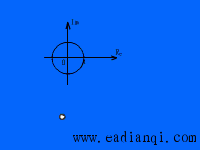
可见,振荡环节的幅频特性同时是角频率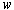 及阻尼比 及阻尼比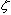 的二元函数,在 的二元函数,在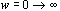 变化时,虽然幅频特性因 变化时,虽然幅频特性因 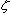 不同而有多条特性曲线,但这些特性曲线都是从1衰减到0。在 不同而有多条特性曲线,但这些特性曲线都是从1衰减到0。在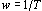 处的幅频特性值为 处的幅频特性值为
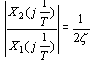
这说明,当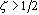 时,幅频特性值 时,幅频特性值 ;当 ;当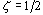 时,该值将等于1;当 时,该值将等于1;当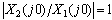 时,该值将大于1,即较 时,该值将大于1,即较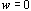 时的 时的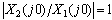 为大,这表明振荡环节在这种情况下产生明显的谐振现象。 自动控制网www.eadianqi.com版权所有 为大,这表明振荡环节在这种情况下产生明显的谐振现象。 自动控制网www.eadianqi.com版权所有


 一阶微分环节的频率响应 一阶微分环节的频率响应
一阶微分环节的传递函数为

式中 —时间常数,量纲为s。由传递函数求得一阶微分环节的幅频及相频特性分别为 —时间常数,量纲为s。由传递函数求得一阶微分环节的幅频及相频特性分别为
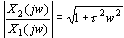 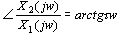
可见在角频率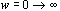 时,一阶微分环节的幅频特性由1变到 时,一阶微分环节的幅频特性由1变到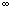 。当 。当 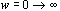 时,一阶微分环节的相频特性由 时,一阶微分环节的相频特性由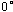 变到 变到 ,即该环节的角频率 ,即该环节的角频率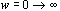 相移发生在正角范围之内。 相移发生在正角范围之内。 本文来自www.eadianqi.com

 二阶微分环节的频率响应 二阶微分环节的频率响应
二阶微分环节的传递函数为

式中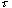 ——时间常数; ——时间常数;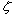 ——阻尼比, ——阻尼比,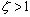 是该环节常用的一种特性,这是二阶微分环节具有两个不等的实零点。 是该环节常用的一种特性,这是二阶微分环节具有两个不等的实零点。 自动控制网www.eadianqi.com版权所有
由传递函数求得二阶微分环节的幅频特性与相频特性为
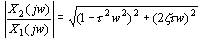 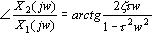
可见,当 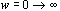 时,二阶微分环节的相移范围是 时,二阶微分环节的相移范围是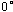 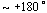 。 。


 不稳定惯性环节的频率响应 不稳定惯性环节的频率响应 本文来自www.eadianqi.com
不稳定惯性环节传递函数为
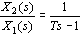
式中T——代表惯性的时间常数。由传递函数求得不稳定惯性环节的幅频特性和相频特性为
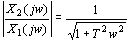 
可见不稳定惯性环节与普通的惯性环节具有相同的幅频特性,当角频率 时,不稳定惯性环节的相移范围是 时,不稳定惯性环节的相移范围是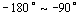 。 。
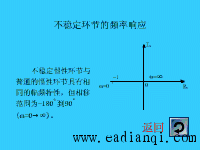
 自动控制网www.eadianqi.com版权所有
 时滞环节的频率响应 时滞环节的频率响应
时滞环节的传递函数为
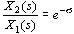
式中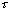 ——时滞环节的时滞,量纲为s。由传递函数求的时滞环节的频率响应为 ——时滞环节的时滞,量纲为s。由传递函数求的时滞环节的频率响应为
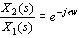
可见时滞环节的幅频特性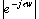 等于与角频率 等于与角频率 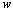 无关的常量1,其相频特性为与 无关的常量1,其相频特性为与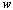 成正比的负相移。 本文来自www.eadianqi.com 成正比的负相移。 本文来自www.eadianqi.com
|
 Nyquist图
Nyquist图
 放大环节的频率响应
放大环节的频率响应
 积分环节的频率响应
积分环节的频率响应
 惯性环节的频率响应
惯性环节的频率响应
 振荡环节的频率响应
振荡环节的频率响应

 一阶微分环节的频率响应
一阶微分环节的频率响应
 二阶微分环节的频率响应
二阶微分环节的频率响应
 不稳定惯性环节的频率响应
不稳定惯性环节的频率响应 
 时滞环节的频率响应
时滞环节的频率响应