|
异步电机的数学模型比较复杂,坐标变换的目的就是要简化数学模型。第6.6.2节的异步电机数学模型是建立在三相静止的ABC坐标系上的,如果把它变换到两相坐标系上,由于两相坐标轴互相垂直,两相绕组之间没有磁的耦合,仅此一点,就会使数学模型简单了许多。
1.异步电机在两相任意旋转坐标系(dq坐标系)上的数学模型
两相坐标系可以是静止的,也可以是旋转的,其中以任意转速旋转的坐标系为最一般的情况,有了这种情况下的数学模型,要求出某一具体两相坐标系上的模型就比较容易了。
变换关系
设两相坐标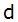 轴与三相坐标 轴与三相坐标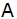 轴的夹角为 轴的夹角为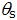 , 而 , 而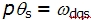 为 为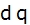 坐标系相对于定子的角转速, 坐标系相对于定子的角转速,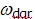 为 为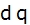 坐标系相对于转子的角转速。 坐标系相对于转子的角转速。 本文来自www.eadianqi.com
|
 |
|
变换过程 自动控制网www.eadianqi.com版权所有
|
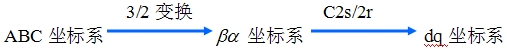 |
|
具体的变换运算比较复杂, |
 |
|
根据式(6-98)另0轴为假想轴d轴和A轴夹角为 θ 可得: |
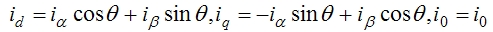 |
|
写成矩阵形式: |
 |
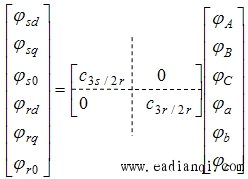
合并以上两个方程式得三相静止ABC坐标系到两项旋转dq0坐标系的变换式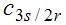 |
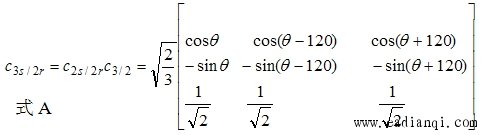 |
|
(1)磁链方程 自动控制网www.eadianqi.com版权所有
利用变换将定子的三项磁链和转子的三项磁链变换到dqo坐标系中去,定子磁链的变换阵是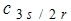 其中d轴与A轴的夹角为 其中d轴与A轴的夹角为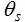 ,转子磁链的变换阵是 ,转子磁链的变换阵是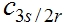 是旋转三相坐标系变换到不同转速的旋转两相坐标系。其中 d 轴与 α 轴的夹角为 是旋转三相坐标系变换到不同转速的旋转两相坐标系。其中 d 轴与 α 轴的夹角为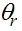 。 自动控制网www.eadianqi.com版权所有 。 自动控制网www.eadianqi.com版权所有
|
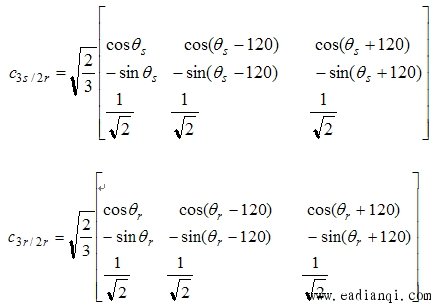 |
|
则磁链的变换式为: |
 |
|
把定子和转子的磁链表达成电感阵和电流向量乘积,在用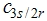 和 和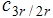 的反变换阵把电流变换到dq0坐标上: 的反变换阵把电流变换到dq0坐标上: 本文来自www.eadianqi.com
|
 |
|
磁链的零轴分量为
它们各自独立对dq轴磁链没有影响,可以不考虑则可以简化。 自动控制网www.eadianqi.com版权所有
|
控制有关。
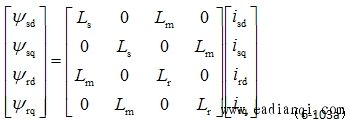
代入参数计算,并去掉零轴分量则dq坐标系磁链方程为 |
 |
|
或写成 |
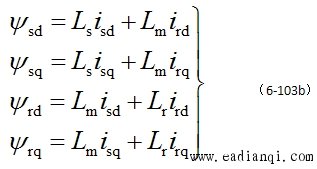 |
|
式中 |
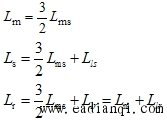 |
—— dq坐标系定子与转子同轴等效绕组间的互感;
—— dq坐标系定子等效两相绕组的自感; 本文来自www.eadianqi.com
——dq坐标系转子等效两相绕组的自感。
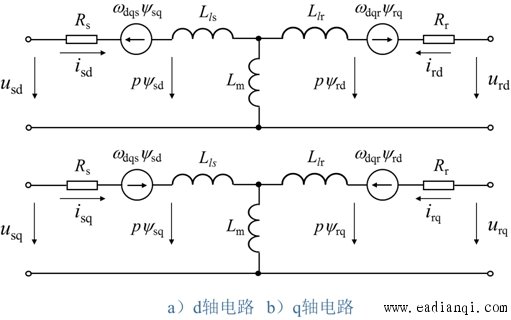
异步电机在两相旋转坐标系dq上的物理模型 |
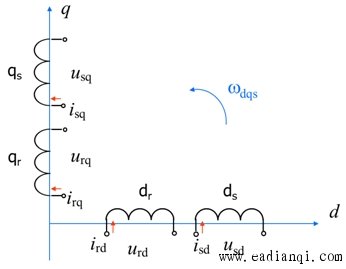 |
|
图6-50 异步电动机在两相旋转坐标系dq上的物理模型 |
(2)电压方程
利用上式A得定子电压变换的关系为 |
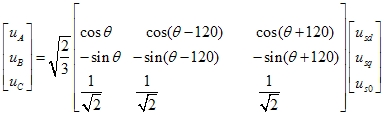 |
先讨论A相的关系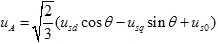 |
同理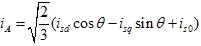 |
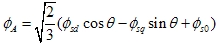 |
|
在ABC坐标系下A相的电压方程, |
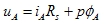 |
代入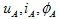 得 得 |
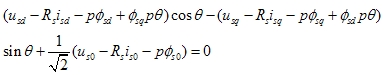 |
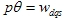 为dq0旋转坐标系对于定子的角速度 为dq0旋转坐标系对于定子的角速度 自动控制网www.eadianqi.com版权所有
由于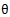 为任意值因此下式三式成立 为任意值因此下式三式成立 |
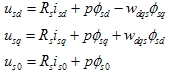 |
|
同理转子电压方程为 |
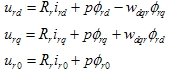 |
式中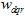 为dq0旋转坐标系相对于转子的角速度 为dq0旋转坐标系相对于转子的角速度 |
同理利用B相和C相的电压方程求出的结果与上面一致。
(2)电压方程
上面的方程整理有定子和转子的电压方程 |
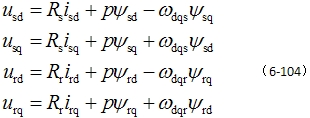 |
 |
|
令 |
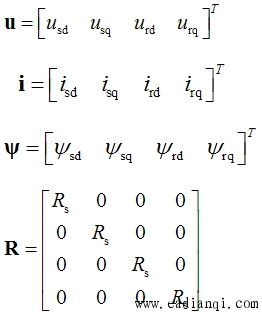 |
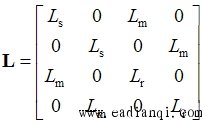 |
|
旋转电动势向量 |
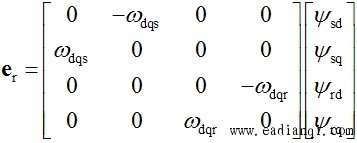 |
|
则式(6-106a)变成 |
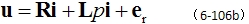 |
|
这就是异步电机非线性动态电压方程式。与第6.6.2节中ABC坐标系方程不同的是:此处电感矩阵 L 变成 4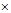 4 常参数线性矩阵,而整个电压方程也降低为4维方程。 4 常参数线性矩阵,而整个电压方程也降低为4维方程。 本文来自www.eadianqi.com
(3)转矩和运动方程 本文来自www.eadianqi.com
|
dq坐标系上的转矩方程为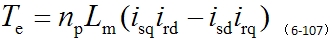
运动方程与坐标变换无关,仍为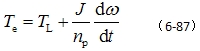
其中 ——电机转子角速度。 ——电机转子角速度。
阶数下降,但非线性、强耦合、多变量性质未变。
异步电机在dq坐标系上的动态等效电路 |
 |
2. 异步电机在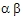 坐标系上的数学模型 本文来自www.eadianqi.com 坐标系上的数学模型 本文来自www.eadianqi.com
在静止坐标系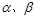 上的数学模型是任意旋转坐标系数学模型当坐标转速等于零时的特例。当 上的数学模型是任意旋转坐标系数学模型当坐标转速等于零时的特例。当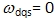 时, 时,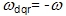 ,即转子角转速的负值,并将下角标 ,即转子角转速的负值,并将下角标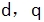 改成 改成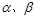 ,则式(6-105)的电压矩阵方程变成 ,则式(6-105)的电压矩阵方程变成 |
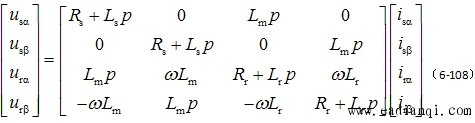 |
|
而式(6-103a)的磁链方程改为 |
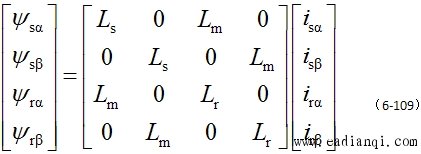 |
利用两相旋转变换阵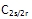 ,可得 ,可得 |
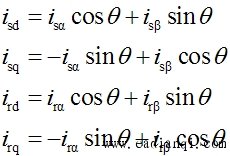 |
代入式(6-107)并整理后,即得到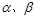 坐标上的电磁转矩 坐标上的电磁转矩 |
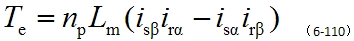 |
|
式(6-108)~式(6-110)再加上运动方程式便成为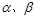 坐标系上的异步电机数学模型。这种在两相静止坐标系上的数学模型又称作Kron的异步电机方程式或双轴原型电机(Two Axis Primitive Machine)基本方程式。 坐标系上的异步电机数学模型。这种在两相静止坐标系上的数学模型又称作Kron的异步电机方程式或双轴原型电机(Two Axis Primitive Machine)基本方程式。 本文来自www.eadianqi.com
3. 异步电机在两相同步旋转坐标系上的数学模型
另一种很有用的坐标系是两相同步旋转坐标系,其坐标轴仍用d,q表示,只是坐标轴的旋转速度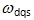 等于定子频率的同步角转速 等于定子频率的同步角转速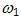 。而转子的转速为 。而转子的转速为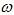 ,因此 dq 轴相对于转子的角转速 ,因此 dq 轴相对于转子的角转速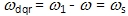 ,即转差。代入式(6-105),即得同步旋转坐标系上的电压方程 ,即转差。代入式(6-105),即得同步旋转坐标系上的电压方程
在二相同步旋转坐标系上的电压方程 自动控制网www.eadianqi.com版权所有
|
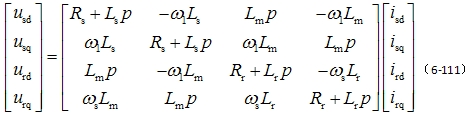 |
|
磁链方程、转矩方程和运动方程均不变。
两相同步旋转坐标系的突出特点是,当三相ABC坐标系中的电压和电流是交流正弦波时,变换到dq坐标系上就成为直流。
4、按转子磁场定向下的数学模型
在dq坐标系放在同步旋转磁场下使d轴与转子磁场的方向重合此时转子的d轴的磁通分量为0,既有下式。带入式(6-111) 本文来自www.eadianqi.com
|
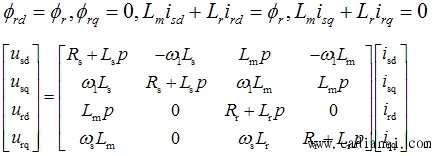 |
三四行出现零元素,减少了耦合,简化了模型
上式中解得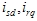 ,带入dq坐标系中的转矩方程有如下结果, ,带入dq坐标系中的转矩方程有如下结果, |
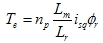 |
|
这个关系和直流电机的转矩方程非常接近了,如果是鼠笼电机结果会更加简单。 本文来自www.eadianqi.com
|